What is Bursty Dynamics?
Bursty Dynamics is a Python package designed to facilitate the analysis of temporal patterns in longitudinal data. It provides functions to calculate the burstiness parameter (BP) and memory coefficient (MC), detect event trains, and visualise results. An event is a timestamped record in the data. A train is a cluster of events that occur in close temporal proximity to each other.
Key Features
Burstiness Parameter (BP) and Memory Coefficient (MC) Calculation: Calculate BP and MC to quantify the irregularity and memory effects of event timing within longitudinal data.
Event Train Detection: Detect and label event trains based on user-defined criteria such as maximum inter-event time and minimum burst size.
Train-Level Analysis: Analyse BP and MC for detected event trains, providing insights into temporal patterns within trains of events.
Visualisation Tools: Visualise temporal patterns with scatter plots, histograms, kernel density estimates (KDE), and more, facilitating interpretation of analysis results.
User-Friendly Interface: Designed for ease of use, with clear function parameters and output formats, making it accessible to both novice and experienced users.
What is Burstiness parameter?
Burstiness parameter is a quantitative measure of the irregularity of events occurring over time. The burstiness parameter is measured using the mean (μ) and standard deviation (σ) of the inter-event time distribution as shown in the equation below.
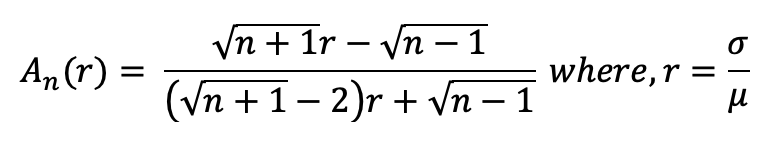
The score ranges between -1 and 1, where a score closer to -1 indicates more regular intervals between events, a score near 0 suggests a random distribution of events, and a value score to 1 indicates a more severe burst pattern, when σ→∞, characterized by rapid, intense occurrences of events. This score is crucial in differentiating between regular, random, and bursty time series. We use the measure, burstiness parameter A, defined by (Kim and Jo, 2016) as an extension of (Goh and Barabasi, 2008) that accounts for the varying length of events.
One important aspect to note is that the burstiness measure is invariant under scaling and translation of the underlying times. Regularly spaced events across days, months or years will have the same measure of burstiness.
What is Memory Coefficient?
The memory coefficient is a statistical measure used to understand the temporal structure of the sequence of events. This coefficient, denoted as M, is calculated using the Pearson correlation formula between successive interevent times (T_i) within a given data sequence.
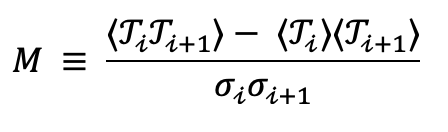
M ranges from -1 to 1, where a positive M suggests a correlation in the interevent times (i.e., long times follow long times and short times follow short times), a negative M implies an alternating pattern between long and short interevent times, and an M of 0 indicates no correlation.
What is Train Detection?
Inspired by the work of Corner et al. (2002), we are implementing a technique to identify clusters of events, known as train detection. This method focuses on detecting clusters of closely spaced events within longitudinal data. In this context, a "train" refers to a sequence of events occurring in close temporal proximity, indicating a period of heightened activity. For a series of events to be considered a train, the time intervals between consecutive events must be shorter than or equal to a predefined threshold (maximum inter-event time), and there must be at least a minimum number of events in the sequence.
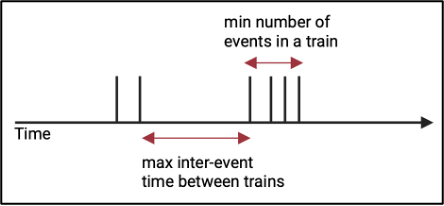
Maximum Inter-Event Time Threshold: This threshold sets the maximum allowable time gap between consecutive events for them to be considered part of the same train. If the time gap between two successive events exceeds this threshold, the second event is not included in the current train, marking the end of that train.
Minimum Number of Events Threshold: This threshold ensures that a train has enough events to be considered significant. It sets the minimum number of events required for a sequence to qualify as a train.
References
Corner, M.A. et al. (2002) 'Physiological effects of sustained blockade of excitatory synaptic transmission on spontaneously active developing neuronal networks—an inquiry into the reciprocal linkage between intrinsic biorhythms and neuroplasticity in early ontogeny,' Neuroscience & Biobehavioral Reviews/Neuroscience and Biobehavioral Reviews, 26(2), pp. 127–185. https://doi.org/10.1016/s0149-7634(01)00062-8.
Goh, K., & Barabási, A. (2008). Burstiness and memory in complex systems. Europhysics Letters, 81(4), 48002. https://doi.org/10.1209/0295-5075/81/48002
Kim, E., & Jo, H. (2016). Measuring burstiness for finite event sequences. Physical Review. E, 94(3). https://doi.org/10.1103/physreve.94.032311